单目双目深度估计论文解读：Two-in-One Depth

		发表于: 2024-12-19 11:19:00 | 已被阅读: 150 | 分类于: 12

单目双目深度估计论文解读：Two-in-One Depth: 单目双目混合自蒸馏训练

原论文：点我

做了什么

提供了一种高效的单目，双目深度估计混合训练方法，最终得到的网络既可以单目预测，也可以双目预测。

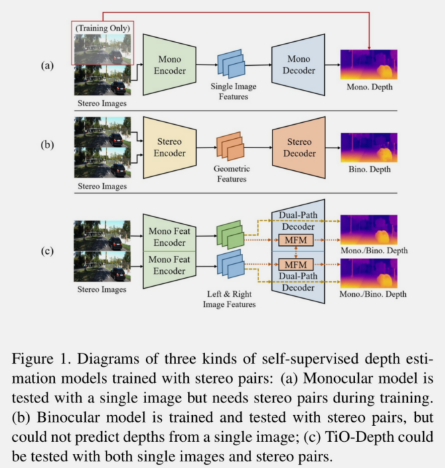
网络核心结构

编码器输出多个分辨率的特征
SDFA模块可以执行类似上采样的功能，把相邻两个分辨率的特征层融合，级联3个 SDFA 模块
执行双目预测和训练时，使用 MFM 模块融合左右视图的特征

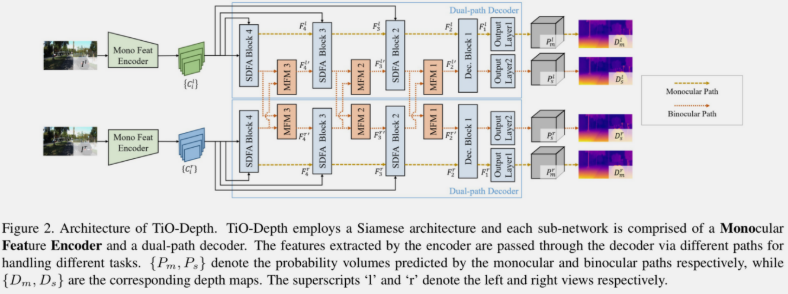
上图中的两个子网络共享参数。

单目路线

以最后一级的 SDFA 模块输出特征作为输入，使用 Dec Block 和 Output Layer 1 输出左视图的 $ P_m^l $（视差概率张量，论文称为”probability volumes“），然后计算出深度图 $ D_m^l $。

双目路线

在单目路线的基础上，在 Dec Block 之后多了一个 Output Layer 2，输出预测的右视图的视差概率 $ P_m^r $，最终计算出深度图 $ D_m^r $。

视差概率

Output Layer 1/2 生成离散的视差张量 $ V \in R^{N \times H \times W} $，$ N $ 是预设的离散等级，这里解释下 $ N $：预设了最大视差和最小视差后，可以得到视差范围，$ N $ 表示将视差范围按照指定方法划分 $ N $ 个值，第$ n $个值记为 $ b_n $：

$$ b_n = d_{max}(\frac{d_{min}}{d_{max}})^{n/(N-1)} $$

根据前人研究，定义了离散深度约束（discrete depth constraint）：与深度负相关的视差可以表示为若干离散视差的加权和，所以事先划分好 $ N $ 个区间后，只需再预测出输入图像的各个像素的权重（视差张量 $ V $ 通过 softmax 操作可以得到这个权重），就可以得到各个像素的视差 $ d $ 了。

$$ d = \sum_{n=0}^{N-1}{softmax(V, dim=通道维度) \odot b_n} $$

$ \odot $ 表示逐元素的乘法，深度值 $ D $ 可以根据基线 $ B $ 以及 $ x $ 轴方向的焦距计算：$ D = (B\cdot f_x)/d $。

论文还定义了连续深度约束（continuous depth constraint）：每个像素的深度值是一个连续变量。

不过个人认为离散/连续深度约束这两个定义并没有什么实际价值，在论文中只是两个名称而已。

`MFM`模块

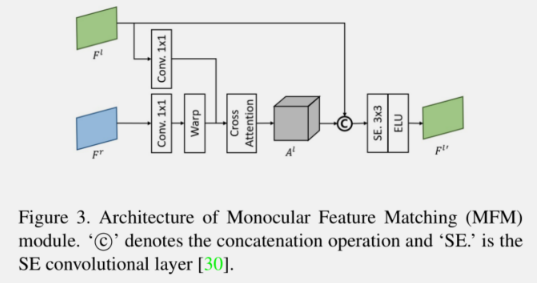
核心结构是使用了交叉注意力机制生成 cost volume（不是很好翻译，它类似于前面提到的”视差概率“） $ A^l $。具体为：使用 $ 1\times1 $ 卷积分别生成左视图的查询特征 $ Q^l $ 和右视图的键特征 $ K^r $，使用缩放的 $ b'_n = \frac{W'}{W}b_n $ 对 $ K^r $ 做 $ N $ 次偏移可以得到一组键特征 $ K^r_n $ ，使用查询特征和第 $ n $ 次偏移的键特征可计算第 $ n $ 个 score map：

$$ S_n^l = \frac{sum(Q^l \odot K_n^r)}{\sqrt C} $$

其中 $ C $ 和$ W $分别是输入特征 $ F^r $ 与$ F^l $ 的通道数和宽度，，$ sum() $ 表示沿着通道维度求和，通过拼接 $ S_n^l $ ，并沿着通道维度做 $ softmax $ 得到最终的 cost volume $ A^l \in R^{N\times H' \times W'} $ ：

$$ A^l = softmax \left( cat(\{S^r_n\}_{n=0}^{N-1}) \right) $$

将左视图的特征 $ F^l $ 和 $ A^l $ 拼接，再经过 $ SE $ 卷积模块即可获得融合后的特征：

$$ F^{l'} = SE(cat(A^l, F^l)) $$

这个模块也是可以形象理解的：通过对右视图特征 $ F^r $ 各个像素做多次的预设偏移，总有某些预设偏移是接近真实偏移（视差）的，再从左视图特征 $ F^l $ 构建查询特征，最终生成的 $ A^l $ 可看作是从各个像素的 $ N $ 个预设偏移的查询的视差概率。

训练

训练过程分3个阶段进行：

训练阶段1：单目训练
训练阶段2：结合单目训练的结果，执行双目训练
训练阶段3：结合前面两个阶段的训练结果，构建更加可靠的教师预测，训练出性能更加优秀的单目结果，因为使用自身制作教师预测，所以该过程被称作”自蒸馏“

注意，Figure 2 中画的图其实不完整，在单目深度训练时，实际上作者使用了不同的偏移学习分支预测了两个张量，论文中被称为辅助张量 $ V_a $ （只在训练时使用）和最终张量 $ V_m $，分别可以在不同 steps 使用图像光度损失（photometric loss）和蒸馏损失训练。单目预测最终使用 $ V_m $ 计算深度值。辅助张量 $ V_a $ 主要参与前两个阶段的训练，$ V_m $ 则在训练阶段3使用自蒸馏的方式训练。

训练阶段1

使用右视图的辅助张量 $ V_a^r \in R^{N\times H \times W} $可以得到右视图各个像素的视差，结合右视图真实图像$ I^r $，可以得到左视图的重构图像 $ \tilde{I_a^l} $。具体来说，将右视图的辅助张量 $ V_a^r $ 的第 $ n $ 个通道偏移 $ b_n $，可以得到左视图的辅助张量 $ \hat{V_a^l} $，然后对 $ \hat{V_a^l} $ 沿着通道维度做 softmax操作生成对应的视差概率张量 $ \hat{P_a^l} $，左视图的重构图像可以按以下方式得到：

$$ \tilde{I^l} = \sum_{n=0}^{N-1}{\hat{P_{an}^l} \odot I_n^r } $$

$ I_n^r $ 是偏移 $ b_n $ 的左视图，使用真实的左视图 $ I^r $ 作为左视图重构图像的标签，论文构建了损失函数

$$ L_M=L_{rec1}+\lambda_1L_{smo1} $$

训练除了 MFM 模块之外的所有网络参数。

训练阶段2

使用右视图的真实图像 $ I^r $ 和预测的左视图的深度图 $ D_s^l \in R^{1\times H \times W} $，可以计算出左视图的重构图像 $ \tilde{I_s^l} $。设 $ p \in R^2 $ 是左视图图像中的像素坐标，那么结合 $ D_s^l $ 便可以在右视图中找到对应的坐标 $ p' $：

$$ p' = p - \left[\frac{B \cdot f_x}{D_s^l(p)}, 0\right]^T $$

个人认为这里实际上构建的是一个理想情景：认为左右视图已经严格水平对齐，因此视差仅体现在 $ x $ 轴方向上。在工程化时，需结合相机的外参做极线矫正之类的操作，或者构建一种更加可靠的坐标变换方式。

通过将右视图图像中 $ p' $ 处的像素值赋值到左视图重构图像的 $ p $ 处，即可得到重构的左视图图像$ \tilde{I_s^l} $。

在本阶段的训练中使用了上一阶段的训练结果，动机是符合直觉的：在双目成像的左右视图中，因为视角因素，多少会存在一些在左/右视图中可以看到，但是在右/左视图中看不到的像素（后面称为遮挡像素），这些像素在双目估计深度时是不该参与一般的损失计算的。而单目预测就不存在这样的问题，所以本训练阶段并没有使用完整的左视图真实图像 $ I^l $做标签，而是使用了处理过的左视图图像 $ I^{l'} $作为标签图像：

$$ I^{l'} = M_{occ}^l \odot I^l + (1 - M_{occ}^l) \odot \tilde{I_a^l} $$

也即：将$ I^l $中的遮挡像素使用基于单目预测重构的左视图 $ \tilde{I^l_a} $中对应位置的像素替代，其中 $ M^l_{occ} $ 是遮挡掩码：遮挡发生时为0，否则为1。

$ M_{occ} $的计算参考另一篇论文： $$ M(x,y) = \begin{cases} 1 & \min_{i \in (0, W-x)}\left( I_{d}(x+i, y) - I_d(x, y) -i \right) \ge k \ 0 & otherwise \end{cases} $$ $ W $ 是预先定义的搜索宽度，$ k $ 是预设值，$ I_d $ 是视差图。这个定义也是符合直觉的：如果视差图中某个位置的视差变化过快，则认为此处可能是原双目视图中的遮挡像素。

有了重构的左视图图像 $ \tilde{I_s^l} $ 和它的标签图像 $ I^{l'} $，计算损失函数就很简单了，论文如下定义：

$$ L_{rec2} = \alpha ||\tilde I_s^l - I^{l'}||_1 + (1 - \alpha) SSIM(\tilde I_s^l, I^{l'}) $$

$ \alpha $ 是超参数，$ SSIM() $ 用于计算两个图像之间的差异，比较容易实现，本文不赘述。

网络结构中的3个 MFM 模块生成的3个 $ \{A_i^l\}_{i=1}^3 $ 通过单目训练中的辅助张量生成的概率张量 $ P_a^l $ 引导训练：

$$ L_{cos}=\sum_{i=1}^{3}{\frac{1}{\Omega}_i \sum_{||A_i^l(x) - P_a^l\left||_1 > t_1}} {||A_i^l(x) - P_a^l\left||_1} $$

$ \Omega_i $ 表示 $ A_i $ 中有效的 $ x $ 坐标数量，$ t_1 $ 是预设值，$ \left< \right> $ 表示双线性采样。

论文还从梯度上，以及单目训练中的辅助视差图的边缘区域定义了视差引导损失，以提升双目训练的性能：

$$ L_{gui} = ||\partial_x d_a^l - \partial_x d_s^l||_1 + ||\partial_y d_a^l - \partial_y d_s^l||_1 + M_{out}^l \odot ||d_a^l - d_s^l||_1 $$

其中的 $ M_{out} $ 是表示重投影坐标是否位于图像外部的掩码，是则为1，否则为0。最终，训练阶段2的损失为：

$$ L_S = L_{rec2} + \lambda_2 L_{smo2} + \lambda_3 L_{cos} + \lambda_4 L_{gui} $$

在本阶段，只有双路 decoder 模块的参数被优化，encoder 的参数保持不变。

训练阶段3

这一步骤的关键内容就是结合前面两个阶段的训练结果，构建尽量准确的视差概率作为教师信号，优化单目训练中的 $ V_m $，目的是获得更加准确的单目估计。论文首先计算半物体边缘图（half-object-edge map）$ M^l_{hoe} $用于指示像素该使用单目估计还是双目估计，$ M_{hoe}^l $ 是一个灰度图，按照以下方式计算：

$$ M_{hoe}^l = M_{occ'}^l \odot min \left( \frac{maxpool(||k * D_s^l||_1)}{t_2}, 1 \right) $$

$ maxpool() $ 是 $ 3\times3 $ 步进 1 的最大池化，$ k $ 是 $ 3\times3 $ 的拉普拉斯算子核，使用拉普拉斯核对深度图 $ D_s^l $ 进行卷积再计算 $ L1 $，得到梯度幅值，最大超计划可以增强区域的梯度响应，$ t_2 $ 可看作是温度系数，$ min() $ 将值控制在 $ [0, 1] $ 范围内。

$ M_{occ'}^l $ 表示反掩码，它可以消除由于遮挡导致的不可靠深度信息，通过将左视图的视差当作右视图的视差计算而来。

$ M_{hoe}^l $ 的意义也是形象的，它核心是突出深度变化剧烈的区域，例如物体的边缘，前文已经分析过，在物体的边缘，双目估计因为视角的原因，通常不准确。所以 $ M_{hoe}^l $ 指示了输入图像各个像素的深度估计是双目估计准确，还是单目估计准确，此时结合前2个训练阶段的结果，可以得到更加准确的混合视差概率：

$$ P_h^l = (1 - M_{hoe}^l) \odot P_S^l + M_{hoe}^l \odot P_a^l $$

$ P_h^l $ 可认为是前两个训练阶段共同获得的更加精确的教师信号，它用于指导 $ V^l_m $ 的训练，损失函数可使用 $ KL $ 散度定义，以拉近 $ P^l_m = softmax(V^l_m, dim=通道维度) $ 与 $ P_h^l $：

$$ L_{dis} = KL(P_h^l || P_m^l) $$

这一训练阶段仅优化 SDFA ，decoder 模块以及 $ Output Layer $ 的参数。

结果

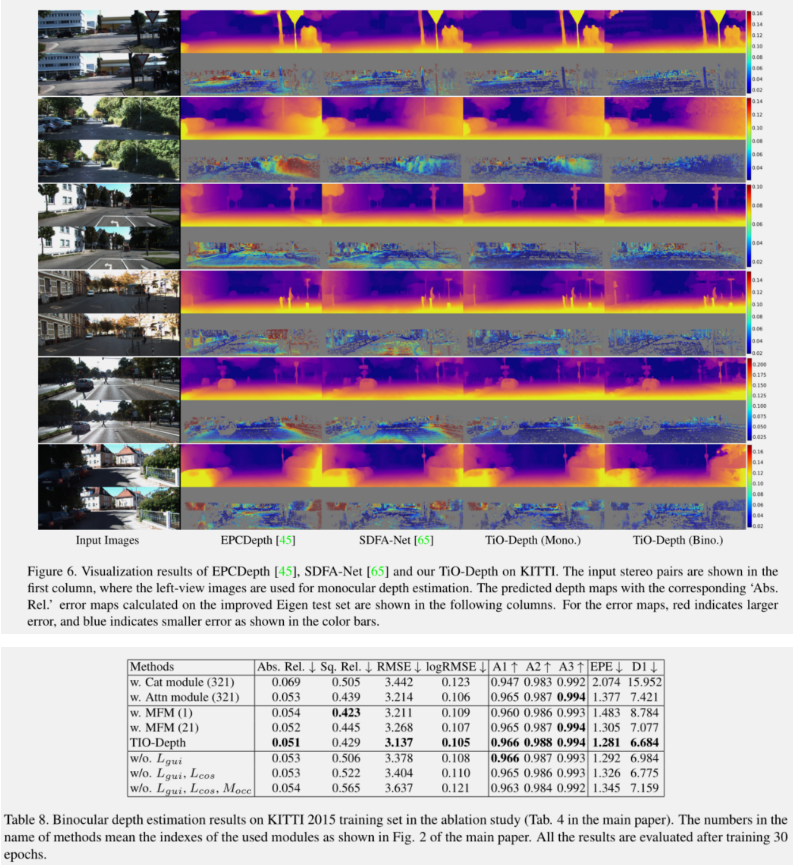
结果还不错，尤其在灌木丛的估计中，层差感被估计出来了。