上一节介绍了算法的概念，讨论了算法与程序开销，以及程序工作效率之间的关系，并且在最后给出了一道面试题，要求使用C语言写出几种常用的数组排序算法，并比较各种方法的工作效率。限于篇幅，上一节主要讨论了插入排序法，本节我们再来看看其他几个常用的数组排序算法。
当然了，为了让文章不至于空洞，本节仍然以分析知名公司面试题的形式，讨论另外几种常用的数组排序算法。
冒泡排序法
提到数组排序，就不得不说一下冒泡排序法，这个排序法的名字比较有趣，属于非常基础的排序算法，常作为C语言初学者的编程练习题出现。不过，虽然比较基础，冒泡排序法也常常出现在各大公司的面试题中，例如，中国著名通信企业H公司有道面试题如下：
请用 C 语言写出一个冒泡排序程序，要求输入10个整数，输出排序结果。
将数组 list 中的每个元素看作是密度为 list[i] 且互不相溶的液体，按照物理学定律，密度小的液体总是会上浮到密度大的液体之上，这一过程看起来就像是气泡从水底漂浮到水表面一样，因此参考照顾原理实现的数组排序法称为“冒泡排序法”。
现在细化“密度小的液体上浮到密度大的液体之上”这一过程，应该能发现，上浮中的液体总是和它旁边的液体相比较，若是发现对方密度比自己大，就继续上浮，一直上浮到密度比自己小的液体或者最上端为止。使用C语言模拟这一过程，其实就是比对两个数组元素大小，并在合适的时候交换相邻元素的值而已，相关C语言代码很简单：
if(list[j]>list[j+1]){
tmp = list[j];
list[j] = list[j+1];
list[j+1] = tmp;
}
将上述过程应用到整个数组，就能实现一次完整的冒泡排序了，相关C语言代码如下，请看：
void bubbling_sort(int *list, int len)
{
int i, j , tmp;
for(i=0; i<len-1; i++){
for(j=0; j<len-1-i; j++){
if(list[j]>list[j+1]){
tmp = list[j];
list[j] = list[j+1];
list[j+1] = tmp;
}
}// for(j=0; j<len...
}
}
在 main() 函数中初始化乱序排列的 10 个元素的数组 list，调用 bubbling_sort() 函数测试之，发现输出与预期一致：
# gcc t.c
# ./a.out
0 1 2 3 4 5 6 7 8 9
冒泡排序可以纳入交换排序，基本思想都是两两比较待排序的数组元素，若发现元素次序相反就立即交换之，直到没有数组中反序排列的元素为止。
快速排序法
基于交换排序思想的另一个典型排序方法是快速排序法，从方法名字就能看出这是一种比较快速的方法，的确如此，快速排序法的效率常常比冒泡排序法高很多。
快速排序法不再比较数组的相邻元素了，而是从数组中找出一个元素值作为基准值，然后将数组中的其他元素与之比较，然后将数组中小于基准值的元素全部移到基准值的左边，大于基准值的元素则全部移到右边。例如，对数组 list 排序：
int list[10] = {4, 2, 1, 5, 9, 6, 3, 8, 0, 7};
假设选取 4 作为基准值，设定两个索引指针 i 和 j，i 从数组左往右移动(i=0; j++;)，j 从数组右往左移动 (j=9; j--;)，如上图，快速排序可如下进行：
* 移动 j，找出小于 4 的数值并记录其位置，显然是 0(list[8])；
* 移动 i，找出大于 4 的数值并记录其位置，显然为 5(list[3])；
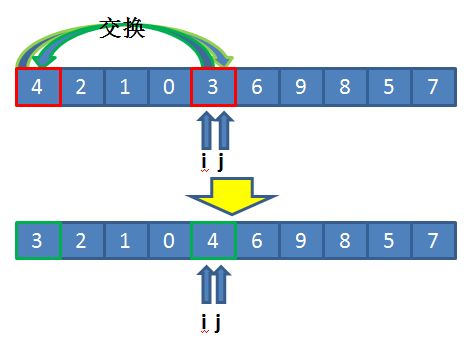
* 交换 list[3] 和 list[8] 的数值，此时 list 的数值为 {4, 2, 1, 0, 9, 6, 3, 8, 5, 7}。
继续上述操作，发现需要交换 3(list[6]) 和 9(list[4])，得到：
{4, 2, 1, 0, 3, 6, 9, 8, 5, 7}
继续上述操作，移动 j 发现了小于 4 的数值 3(list[4])，再移动 i 发现 i 与 j 相遇了。此时应该交换基准值和6，也即交换 list[0] 和 list[4]，得到：
{3, 2, 1, 0, 4, 6, 9, 8, 5, 7}
可以看出，操作停止后，虽然 list 中小于 4 的元素都在 4 左边，大于 4 的元素都在 4 右边，但是单看左右两边的子数组却仍然是乱序的：
{3, 2, 1, 0}
{6, 9, 8, 5, 7}
不过，只要对左右两个子数组再进行一次上述操作，一直到整个数组排序完毕就可以了。显然，利用递归非常容易解决这类问题。
关于递归，前面两节已较为详细的讨论，感到陌生的朋友可以翻回去看看。
现在知道了快速排序的基本原理了，再来看个面试题，下面这道题出自美国某著名计算机嵌入式公司：
下面这段C语言代码是实现快速排序的函数，补全最后的代码。
void improveqsort(int *list, int m, int n)
{
int k,t,i,j;
if(m<n){
i = m;
j = n+1;
k = list[m];
while(i<j){
for(i=i+1; i<n; i++)
if(list[i]>=k)
break;
for(j=j-1; j>m; j--)
if(list[j]<=k)
break;
if(i<j){
t = list[i];
list[i] = list[j];
list[j] = t;
}
}
t = list[m];
list[m] = list[j];
list[j] = t;
improveqsort( , , ); /* 补全参数 */
improveqsort( , , ); /* 补全参数 */
}
}
如果理解了上文对快速排序法的分析，要解这道题就不难了，请继续往下看。
显然，improveqsort() 函数是一个递归函数。观察 improveqsort() 函数的参数，推测它应该可以完成数组 list 第 m 个到第 n 个元素的排序。
下面为了分析方便，以上图中的行号为准。
第 7 行的 if(m<n) 限定了 improveqsort() 函数只对长度大于 1 的数组排序，若输入的数组长度小于 1，则函数就直接退出了，这其实就是前面两节中提到的“递归函数退出条件”。
第 10 行选定了数组的第 m 个元素作为基准值 k，第 8 到第 23 行就是在 i 遇到 j 之前的交换处理。当 i j 相遇后， improveqsort() 函数开始执行第 24 行到第 26 行，也即交换 j 和 m 处的值。
对照前文的分析，执行完第 26 行代码后，数组 list[m~n] 中小于 list[m] 的数值全部被移到 list[m] 左边，大于 list[m] 的数值则全部被移到 list[m] 右边了。此时需要对左右两个“子数组”进一步做快速排序，因此面试题的代码给出了两次 improveqsort() 函数的调用。那么传递给它们的参数应该是什么呢？
参考上图，再结合前面两节对递归函数的讨论，应该明白基准值的左子数组的索引范围应该是 list[m, j-1]，基准值的右子数组索引范围应该是 list[i, n]，因此补全上述C语言代码的答案应该是：
improveqsort(list, i, n);
improveqsort(list, m, j-1);
并且两句代码不分前后。现在在 main() 函数中调用补全后的 improveqsort() 测试：
int main()
{
int list[10] = {9, 4, 2, 1, 5, 6, 3, 8, 0, 7};
int i;
improveqsort(list, 0, 9);
for(i=0; i<10; i++)
printf("%d ", list[i]);
printf("\n");
return 0;
}
编译上述C语言代码并执行，发现输出与预期一致：
# gcc t.c
# ./a.out
0 1 2 3 4 5 6 7 8 9
其实，快速排序法是基于一种叫做“二分”的思想，类似的还有归并排序法，在我之前的文章里分析过，感兴趣的可以去看看。
小结
利用C语言解决问题的方法常常不止一种，这两节介绍的几种数组排序法就是一个例子。为什么要像孔乙己那样研究“茴”字有几种写法呢？这是因为计算机的运算速度并不是无限快，存储空间也不是无限大。冒泡排序法的确非常简单，但是它的执行效率却比较低，只适合处理较短的数组排序。
按平均时间复杂度可以将数组排序法分为以下几类：
* 平方阶排序：一般称为简单排序，典型例子有插入排序、冒泡排序；
* 线性对数阶排序：如快速排序，归并排序；
* 幂阶排序：如希尔排序；
* 线性阶排序：如桶、箱等以空间换时间的排序法。
应明白，不能简单认为某种排序算法一定比其他排序法好，可能在数学上某种算法的确很具效率，但是在实际中还要考虑计算机的实际运算速度以及存储空间，很有时间效率的算法可能是牺牲了大量存储空间换来的。应在不同条件下，选用不同的排序法，例如：
* 若数组长度很短（如小于50），可采用插入排序法
* 若数组基本有序，可采取冒泡排序
* 若数组较长，选择快速排序或者归并排序则比较合适
