我要努力工作，加油！
文章目录

C语言面试题详解第17节

		发表于: 2019-04-28 08:12:59 | 已被阅读: 28 | 分类于: C语言

上一节介绍了C语言程序开发中常用的数据结构链表，知道了链表特别适合用于处理数量会动态变化，并且允许线性遍历的数据。其实不止如此，

数据结构决定算法的设计，有什么样的数据结构，就可以使用什么用的算法
，本节再来一起看看C语言程序开发中另外一种常用的数据结构——栈，并且本节将以一个有趣的小例子来解释数据结构与算法的关系。

基础数据结构——栈

在之前的章节，我们其实已经对栈这种数据结构有了初步认识，栈是一种类似数组的数据结构，存储一系列数据。不同的是，数组元素的访问可以是随机的，比如这次访问 a[7]，下次访问 a[3]，而栈的访问只能以两种方式：push 和 pop 操作。

可以将栈比作一个圆柱形有底的容器（例如杯子），要存放到栈中的元素比作是一个个刚好能够放入容器的小球，则 push 操作就是将小球放入容器，pop 操作是从容器顶部取出小球。显然，最后放入容器的小球会最先被取出来，换句话说，每次只能操作栈顶的元素。使用C语言编写程序模拟栈的 push 和 pop 操作是简单的，请看如下C语言代码：

char stack[128];
int top = 0;

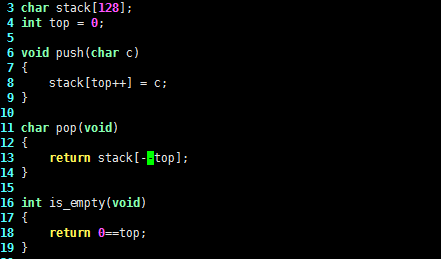
上面这两行 C语言代码把数组 stack 当作栈，top 则表示栈顶的位置。push 和 pop 操作的C语言代码实现也是简单的，请看：

void push(char c)
{
    stack[top++] = c;
}
char pop(void)
{
    return stack[--top];
}
int is_empty(void)
{
    return 0==top;
}

从上面的C语言代码可是看出，push 和 pop 每次操作的都是 stack 的第一个未被栈元素占据的位置，这模拟了“每次只操作栈顶元素”。从 is_empty() 函数的C语言代码可以看出，如果 top 等于 0，表示栈顶和栈底重合，说明此时栈中没有元素，是空的。

现在在 main() 函数中调用测试以上函数，相关C语言代码如下，请看：

#include <stdio.h>
int main()
{
    push('x');
    push('y');
    push('z');

    while(!is_empty())
        putchar(pop());
    putchar('\n');

    return 0;
}

编译并执行这段C语言程序，得到如下输出：

# gcc t.c 
# ./a.out 
zyx

压栈顺序是 x,y,z，出栈顺序是 z,y,x，与预期一致。也许你会说，这不就是把数组倒序打印吗，随便写个循环不就可以了吗：

for(i=len-1; i>=0; i--)
    putchar(stack[i]);

对于数组来说的确没有必要那么复杂，但是这里的 stack 还有另一层含义（栈），上面使用C语言模拟栈操作是为了介绍“栈”这种编程思想，下面来看一个例子。

深度优先搜索

下面这个问题比较有意思，我在求职时，曾经在某著名科技公司的笔试题中遇到过这个问题，请看：

定义一个二维数组 maze，使用 maze 表示一个迷宫：'o' 表示路，'+' 表示墙，左上角是入口，右下角是出口，只能横着或竖着走，不能斜着走，编写C语言程序从迷宫入口走到出口。 
char maze[5][5] = {
    'o', '+', 'o', 'o', 'o',
    'o', '+', 'o', '+', 'o',
    'o', 'o', 'o', 'o', 'o',
    'o', '+', '+', '+', 'o',
    'o', 'o', 'o', '+', 'o',
};

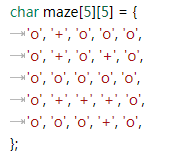
先不考虑C语言编程，想象一下自己要挑战这个迷宫，似乎我能做的只有顺着有路的路线走下去，遇到死路就折回来换个路线，只要有正确路线，而且我不迷路，就一定能走到出口，所以关键点就是
不迷路
。

使用C语言编程模拟上面的过程很简单，无非就是判断上下左右是否 'o'，若是则说明有路，可以走。当然了，关键点在于要

记录已经走过的路线
，这样才能在遇到死路的时候折返回来。现在思路清晰了，写出相关的C语言程序就简单了，首先，因为要解决的问题是一个二维问题，所以为了方便描述位置，定义 point 数据结构，相关C语言代码如下，请看：

struct point{
    int row;
    int col;
};

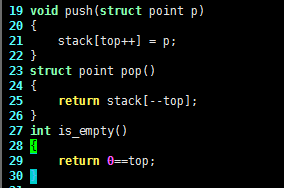
point 可以记录当前在第几行第几列，再定义 statck 和栈顶 top：

struct point stack[128];
int top = 0;

使用栈记录已经走过的路线是方便的，想一下，假设现在在位置 pos1，往下走到 pos2，又往右走到 pos3，发现遇到了死路，这时应该退到位置 pos2，因为 pos2 的左边可能是出口，只有 pos2 的所有方向都是思路，才需要回到 pos1。所以将 push 和 pop 以及 is_empty 的C语言代码写出：

void push(struct point p)
{
    stack[top++] = p;
}
struct point pop()
{
    return stack[--top];
}
int is_empty()
{
    return 0==top;
}

按照前面的思考，假设我们现在在 pos 点，要做的就是判断前后左右是否有路，有路就往下走，所以定义 walk() 函数，它的C语言代码如下，请看：

int walk(struct point p)
{
    struct point next_pos;

    if(4==p.row && 4==p.col)
        return 1;
    if(p.col+1 < 5 && 'o'==maze[p.row][p.col+1]){
        next_pos.row = p.row;
        next_pos.col = p.col+1;
        maze[next_pos.row][next_pos.col] = '*';
        push(next_pos);
    }
    if(p.row+1 < 5 && 'o'==maze[p.row+1][p.col]){
        next_pos.row = p.row+1;
        next_pos.col = p.col;
        maze[next_pos.row][next_pos.col] = '*';
        push(next_pos);
    }
    if(p.col-1 >=0 && 'o'==maze[p.row][p.col-1]){
        next_pos.row = p.row;
        next_pos.col = p.col-1;
        maze[next_pos.row][next_pos.col] = '*';
        push(next_pos);
    }
    if(p.row-1 >=0 && 'o'==maze[p.row-1][p.col]){
        next_pos.row = p.row-1;
        next_pos.col = p.col;
        maze[next_pos.row][next_pos.col] = '*';
        push(next_pos);
    }
    return 0;
}

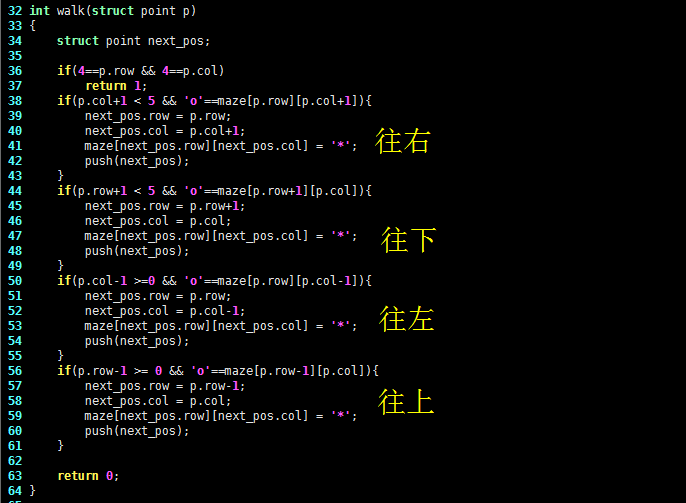
walk() 函数很简单，它首先判断是否已经抵达右下角的迷宫出口，若是则返回 1，否则分别判断右下左上的点是否可以走，如果可以走就将迷宫标记 ' * ’表示已经走过，并将该点压入 stack 记录，如果走到死路，则可以 pop 回到之前的点。

先判断右下，是因为出口在右下方，算法应该偏向此方向。

现在可以写 main() 函数综合处理这些逻辑了，相关C语言代码如下，请看：

int main()
{
    struct point p = {0,0};
    maze[p.row][p.col] = 2;
    push(p);

    while(!is_empty()){
        p = pop();
        if(1==walk(p))
            break;
        print_maze();
    }
    if(is_empty())
        printf("dead maze!\n");

    return 0;
}

上述C语言代码的逻辑很简单，首先把入口点 push 进栈，然后进入 while 循环，如果栈不为空，则循环会一直持续到找到出口，这样一来，在 while 循环之后就可以判断栈是否为空，若不为空则说明找到了合适的路径，否则就说明迷宫是个“死迷宫”，入口到出口之间没有通道。

栈中存放的是C语言程序尝试的路线，最后为空说明程序已经将从起点出发的所有可以走的录像都试探过了，并且仍然没有合适路线。

为了展示C语言程序每一次尝试的过程，上面的 main() 函数中调用了 print_maze() 函数打印迷宫的中间过程，它的C语言代码如下，请看：

void print_maze()
{
    int i, j;
    for (i = 0; i < 5; i++) {
        for (j = 0; j < 5; j++)
            printf("%d ", maze[i][j]);
        putchar('\n');
    }
    printf("--------------\n");
}

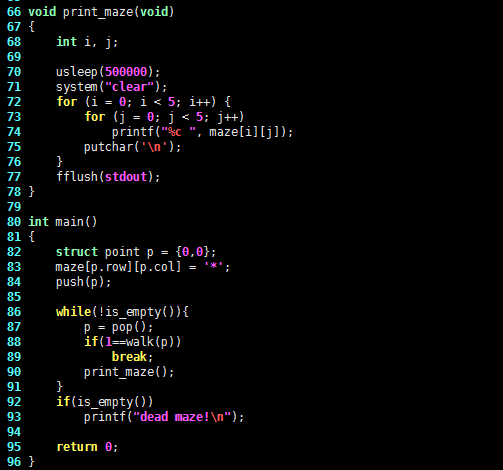
在Linux下，如果希望看到C语言程序找出口的动态过程，可以如下定义 print_maze() 函数，请看：

void print_maze(void)
{
     int i, j;

     usleep(500000);
     system("clear");
     for (i = 0; i < 5; i++) {
         for (j = 0; j < 5; j++)
             printf("%c ", maze[i][j]);
         putchar('\n');
     }
     fflush(stdout);
}

现在编译C语言程序并执行，得到如下结果：

从输出可以看出，C语言程序为了从入口走到出口，基本上把能走的路都走了，但是好在找到了出口。

小结

本节尝试一个有趣的例子说明数据结构与算法设计的关系，为了走出迷宫，我们需要记录已经走过的路线和所有可能有出口的路线，从上面的C语言代码可以看出，使用栈这种数据结构解决此类需求是方便的，而且我们的算法都是围绕栈展开的。由此可以得出，在C语言程序开发中，实际需求决定使用何种数据结构方便，而数据结构则直接决定算法的设计方向。

更多阅读