linux学习第20节，二叉树的特性和插入、查询、删除等基本操作

		发表于: 2019-01-24 19:29:37 | 已被阅读: 24 | 分类于: Linux笔记

前面几节较为详细的讨论了 linux 内核常用的链表、队列、映射等几种数据结构，本节将介绍C语言中另一种重要的数据结构——二叉搜索树（通常简称为BST），并且将一行一行写出相关的C语言代码。

二叉树的概念

树结构是一个多层的特定数据结构，每个节点之间通过指针连接（这点有些像链表），有 1 个或者 0 个入边，和 0 个或多个出边。对于

二叉树

，则每个节点最多只能由 2 个出边，一个典型的二叉树如下图所示。

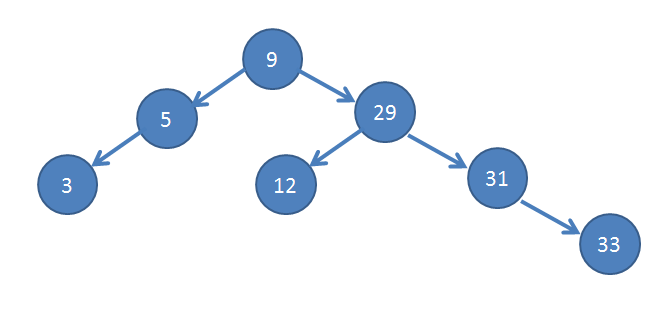
二叉搜索树

如果二叉树的各个节点记录的数值是有序排列的，则该二叉树可称为“二叉搜索树”，它有以下三条性质：

左子节点值都小于根节点值
右子节点值都大于根节点值
所有节点的子树也都是二叉搜索树

能够看出，二叉搜索树其实是“递归”定义的。

因此，二叉搜索树要求在插入数值时保证所有节点都是有序的，即左节点值始终小于父节点值，而右节点值始终大于父节点值。这样一来，二叉搜索树就特别适合存储需要快速检索的数据。

使用C语言描述二叉搜索树

在 C语言中，常常用指针连接二叉树的各个节点，这就和链表很像，所以可以用如下结构体来描述一个二叉树，请看：

typedef struct __BINTREE
{
    struct __BINTREE*   left;
    struct __BINTREE*   right;
    int                 data;
}BINTREE;

BINTREE 结构体非常简单，它有 left 和 right 两个指针，分别指向它的左右两个子节点，还有一个 data 成员用于记录数值。

将数值插入二叉搜索树

现在知道了二叉树的数据结构（BINTREE结构体），如果我想将某个数值插入二叉树，并且还要使其满足“二叉搜索树”的三条性质，该怎样编写C语言代码呢？

前面提到，二叉搜索树的三条性质其实是递归定义的，那么使用C语言的递归函数也就非常容易实现，请看：

int insert_node(BINTREE** pptree, int value)
{
    if(NULL==(*pptree)){
        (*pptree) = (BINTREE*)malloc(sizeof(BINTREE));
        if(NULL==(*pptree)){
            printf("insert %d failed for malloc failed\n", value);
            return -1;
        }
        (*pptree)->data = value;
        (*pptree)->left = (*pptree)->right = NULL;
    }else{
        if(value < (*pptree)->data)
            insert_node(&(*pptree)->left, value);
        else if(value > (*pptree)->data)
            insert_node(&(*pptree)->right, value);
        else
            printf("value %d exist!\n", value);
    }
    return 0;
}

参照二叉搜索树的三条性质，会发现其实 insert_node() 函数非常简单，如果要插入的 value 小于 (* pptree)->data，就将其插入 * pptree 的左子节点，否则将其插入 * pptree 的右子节点。这样一来，二叉树就始终满足二叉搜索树的三条性质了。

关于C语言的递归函数，可以参考这一节。

从二叉搜索树中搜索一个值

因为二叉搜索树是严格有序的，所以从中搜索一个值还是非常简单的，C语言代码可以如下写，请看：

BINTREE* search_node(BINTREE* ptree, int value)
{
    BINTREE* n = ptree;

    while(n){
        if(value > n->data)
            n = n->right;
        else if(value < n->data)
            n = n->left;
        else
            return n;
    }
    return NULL;
}

其实就是将要查询的 value 和树的左右子节点比较而已，如果 value 比节点值大，就继续与右子节点比较，否则就继续与左子节点比较，否则就是 value 等于节点值，即搜索成功，可以返回了。

从二叉搜索树中删除一个节点

以下图中的二叉搜索树为例。要删除的节点分三种情况，情况1：如果要删除的是没有子节点的节点（如3，33），那么直接释放该节点，并让其父节点指向 NULL 即可。情况2：如果要删除的是只有一个子节点的节点（如5，30，31），也是非常简单的，先让父节点指向它的子树，再释放之就可以了。

情况3：如果要删除的是有左右两个子节点的节点（例如9，29），就有些复杂了，因为没法把它的子节点全部挂在它的父节点上。

以删除 29 为例，因为它的父节点 9 已经有另外一个子节点，而 29 有两个子节点，显然是没法直接将其

都

挂在节点 9 上的。

那这种情况该如何处理呢？其实只要使用最接近 29 的节点替换它就可以了，那么谁最接近 29 呢？按照二叉搜索树的性质，最接近 29 的节点，应该是 29 左节点的最右子节点或者 29 右节点的最左子节点。

有了上面的分析，使用 C语言实现从二叉搜索树中删除节点就不难了，请看：

int delete_node(BINTREE** pptree, int value)
{
    BINTREE* dn  = NULL, *sn  = NULL;
    BINTREE* fdn = NULL, *fsn = NULL;
    /** 找到删除节点和它的父节点 */
    dn = *pptree;
    while(dn && value!=dn->data){
        fdn = dn;
        if(value > dn->data)
            dn = dn->right;
        else if(value < dn->data)
            dn = dn->left;
    }
    /** 如果没找到 */
    if(NULL==dn){
        printf("no value %d in bintree\n", value);
        return -1;
    }
    printf("found %d, now delete...\n", dn->data);
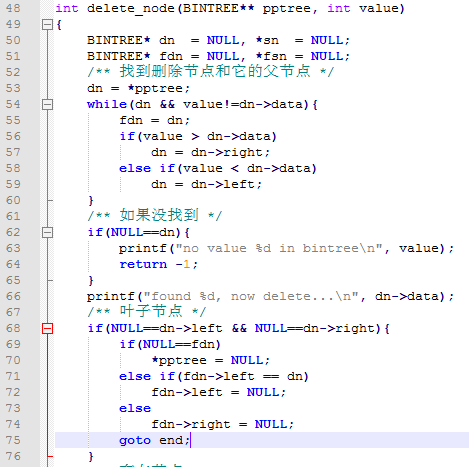
    /** 叶子节点 */
    if(NULL==dn->left && NULL==dn->right){
        if(NULL==fdn)
            *pptree = NULL;
        else if(fdn->left == dn)
            fdn->left = NULL;
        else
            fdn->right = NULL;
        goto end;
    }
end:
    free(dn);
    dn = NULL;
    return 0;
}

根据分析，不管是哪种情况，首先都要找到删除节点和它的父节点。如果删除节点 dn 的左右子节点都为 NULL，则属于情况1，直接释放之并让其父节点指向 NULL即可。再来看看情况2，要删除的节点有一个节点时对应的C语言代码：

    /** 有左节点 */
    if(NULL!=dn->left && NULL==dn->right){
        if(NULL==fdn)
            *pptree = dn->left;
        else if(fdn->left == dn)
            fdn->left = dn->left;
        else
            fdn->right = dn->left;
        goto end;
    }
    /** 有右节点 */
    if(NULL==dn->left && NULL!=dn->right){
        if(NULL==fdn)
            *pptree = dn->right;
        else if(fdn->left == dn)
            fdn->left = dn->right;
        else
            fdn->right = dn->right;
        goto end;
    }

同样是非常简单的，这里就不再赘述了。最后，来看看比较复杂的情况3，要删除的节点有两个子节点，该如何处理呢？按照分析，我们首先应该找替代节点，替代节点可以是要删除节点的左子树的最右节点，也可以是要删除节点的右子树的最左节点，这里使用前者作为要删除节点的替代节点，请看如下C语言代码：

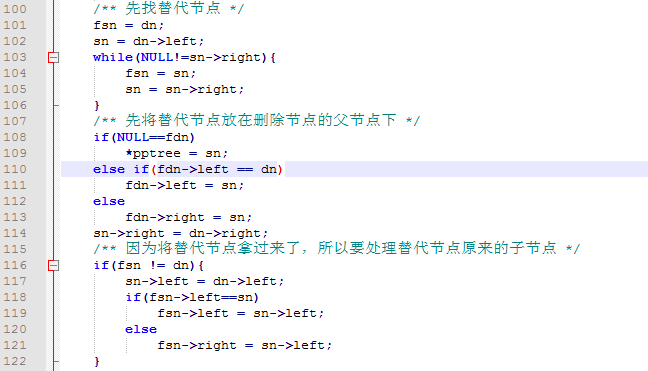
    fsn = dn;
    sn = dn->left;
    while(NULL!=sn->right){
        fsn = sn;
        sn = sn->right;
    }

找到替代节点及其父节点后，我们先用替代节点替换要删除节点，也即让要删除节点的父节点指向替代节点，C语言代码如下，请看：

/** 先将替代节点放在删除节点的父节点下 */
    if(NULL==fdn)
        *pptree = sn;
    else if(fdn->left == dn)
        fdn->left = sn;
    else
        fdn->right = sn;
    sn->right = dn->right;

因为这里使用的替代节点是最右节点，所以它一定没有右子树，但是可能有左子树，这时替代节点已经被拿走替换要删除节点了（和被删除相似），所以它可能的左子树也需要处理一下，请看如下C语言代码：

/** 因为将替代节点拿过来了，所以要处理替代节点原来的子节点 */
    if(fsn != dn){
        sn->left = dn->left;
        if(fsn->left==sn)
            fsn->left = sn->left;
        else 
            fsn->right = sn->left;
    }

这里需要注意的是，要先判断替代节点的父节点是否要删除节点，如果是，就不能进行以下的操作了，否则可能会出现替代节点指向替代节点自己的情况，导致丢失替代节点的可能左子树。

打印二叉搜索树

到这里，二叉搜索树的插入、查询、删除几大基本功能就写好了，检查其是否正确的最好方法就是做实验，那么打印二叉搜索树就是必不可少的了，这里仍然使用递归的方法打印，请看如下C语言代码：

void _print_tree(BINTREE* ptree)
{
    if(NULL!=ptree){
        printf("%d ", ptree->data);
        _print_tree(ptree->left);
        _print_tree(ptree->right);
    }
}
void print_tree(BINTREE* ptree)
{
    printf("\n");
    _print_tree(ptree);
    printf("\n\n");
}

递归函数的“基础条件”就是遍历到 NULL 指针，说明已经到达树的末端了，其他部分就非常简单了。

测试我们编写的二叉搜索树C语言代码

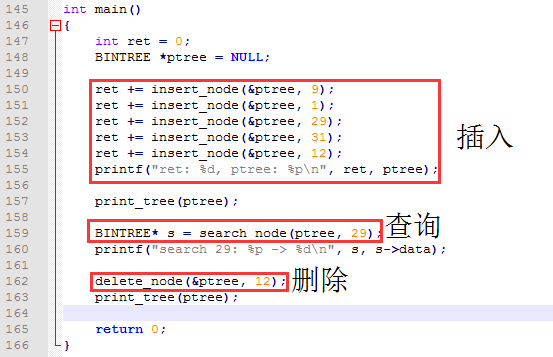
到这里终于可以测试我们编写的二叉搜索树代码了，下面先放入 main 函数的 C语言代码，请看：

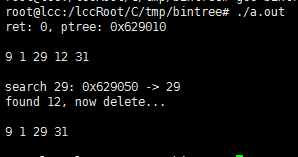
int main()
{
    int ret = 0;
    BINTREE *ptree = NULL;
    ret += insert_node(&ptree, 9);
    ret += insert_node(&ptree, 1);
    ret += insert_node(&ptree, 29);
    ret += insert_node(&ptree, 31);
    ret += insert_node(&ptree, 12);
    printf("ret: %d, ptree: %p\n", ret, ptree);

    print_tree(ptree);

    BINTREE* s = search_node(ptree, 29);
    printf("search 29: %p -> %d\n", s, s->data);

    delete_node(&ptree, 12);
    print_tree(ptree);

    return 0;
}

测试代码很简单，先插入了5个节点到二叉树，然后查询其中的一个节点，再删除一个节点。编译C语言程序，执行结果如下：

一切符合预期，至此，我们就一点一点的完成了二叉搜索树的C语言代码。

附完整代码

代码很简单，就直接放在这里吧。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct __BINTREE
{
    struct __BINTREE*   left;
    struct __BINTREE*   right;
    int                 data;                
}BINTREE;

int insert_node(BINTREE** pptree, int value)
{
    if(NULL==(*pptree)){
        (*pptree) = (BINTREE*)malloc(sizeof(BINTREE));
        if(NULL==(*pptree)){
            printf("insert %d failed for malloc failed\n", value);
            return -1;
        }
        (*pptree)->data = value;
        (*pptree)->left = (*pptree)->right = NULL;
    }else{
        if(value < (*pptree)->data)
            insert_node(&(*pptree)->left, value);
        else if(value > (*pptree)->data)
            insert_node(&(*pptree)->right, value);
        else
            printf("value %d exist!\n", value);
    }
    return 0;
}

BINTREE* search_node(BINTREE* ptree, int value)
{
    BINTREE* n = ptree;

    while(n){
        if(value > n->data)
            n = n->right;
        else if(value < n->data)
            n = n->left;
        else
            return n;
    }
    return NULL;
}

int delete_node(BINTREE** pptree, int value)
{
    BINTREE* dn  = NULL, *sn  = NULL;
    BINTREE* fdn = NULL, *fsn = NULL;
    /** 找到删除节点和它的父节点 */
    dn = *pptree;
    while(dn && value!=dn->data){
        fdn = dn;
        if(value > dn->data)
            dn = dn->right;
        else if(value < dn->data)
            dn = dn->left;
    }
    /** 如果没找到 */
    if(NULL==dn){
        printf("no value %d in bintree\n", value);
        return -1;
    }
    printf("found %d, now delete...\n", dn->data);
    /** 叶子节点 */
    if(NULL==dn->left && NULL==dn->right){
        if(NULL==fdn)
            *pptree = NULL;
        else if(fdn->left == dn)
            fdn->left = NULL;
        else
            fdn->right = NULL;
        goto end;
    }
    /** 有左节点 */
    if(NULL!=dn->left && NULL==dn->right){
        if(NULL==fdn)
            *pptree = dn->left;
        else if(fdn->left == dn)
            fdn->left = dn->left;
        else
            fdn->right = dn->left;
        goto end;
    }
    /** 有右节点 */
    if(NULL==dn->left && NULL!=dn->right){
        if(NULL==fdn)
            *pptree = dn->right;
        else if(fdn->left == dn)
            fdn->left = dn->right;
        else
            fdn->right = dn->right;
        goto end;
    }
    /** 
     * 程序到达这里说明有双子节点 
     * */
    /** 先找替代节点 */
    fsn = dn;
    sn = dn->left;
    while(NULL!=sn->right){
        fsn = sn;
        sn = sn->right;
    }
    /** 先将替代节点放在删除节点的父节点下 */
    if(NULL==fdn)
        *pptree = sn;
    else if(fdn->left == dn)
        fdn->left = sn;
    else
        fdn->right = sn;
    sn->right = dn->right;
    /** 因为将替代节点拿过来了，所以要处理替代节点原来的子节点 */
    if(fsn != dn){
        sn->left = dn->left;
        if(fsn->left==sn)
            fsn->left = sn->left;
        else 
            fsn->right = sn->left;
    }
end:
    free(dn);
    dn = NULL;
    return 0;
}

void _print_tree(BINTREE* ptree)
{
    if(NULL!=ptree){
        printf("%d ", ptree->data);
        _print_tree(ptree->left);
        _print_tree(ptree->right);
    }
}
void print_tree(BINTREE* ptree)
{
    printf("\n");
    _print_tree(ptree);
    printf("\n\n");
}


int main()
{
    int ret = 0;
    BINTREE *ptree = NULL;

    ret += insert_node(&ptree, 9);
    ret += insert_node(&ptree, 1);
    ret += insert_node(&ptree, 29);
    ret += insert_node(&ptree, 31);
    ret += insert_node(&ptree, 12);
    printf("ret: %d, ptree: %p\n", ret, ptree);

    print_tree(ptree);

    BINTREE* s = search_node(ptree, 29);
    printf("search 29: %p -> %d\n", s, s->data);

    delete_node(&ptree, 12);
    print_tree(ptree);

    return 0;
}