发表于: 2020-09-28 08:38:00 | 已被阅读: 155 | 分类于: 算法
		

算法简介

和[广度优先搜索算法][1]一样，深度优先搜索（DFS）算法也是一种图算法，特别适合处理图状的数据结构，如树形数据结构，DFS 从树的根节点开始，沿着给定的路径尽可能的走下去（越走越深），当不能再继续往下走时（稍后将看到实例），DFS 会回溯，选择一条没有走过的路径，继续探索，直到整个树形数据全部被探索出来。

计算机科学中的许多问题都可以用深度优先搜索算法解决，例如分析网络、映射路由、调度和查找生成树都是图问题，要解决这些问题，像深度优先搜索这样的图搜索算法是非常好用的。

我们以更加具体有趣的“迷宫问题”继续探讨深度优先搜索算法。

“迷宫问题”

迷宫游戏是非常好玩的游戏，身在其中不能看到整个迷宫，从入口走到出口，充满一种对“未知”探索的新奇感。

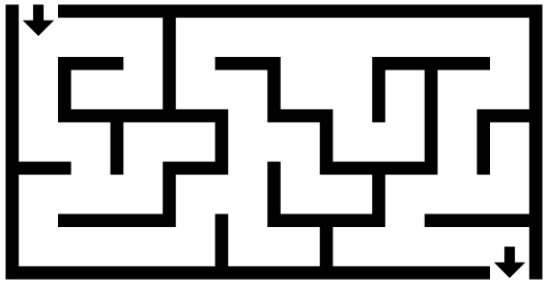
挑战走出迷宫大体上分为两种策略：一是完全凭感觉，多久能走出迷宫完全凭自己的运气。再就是“稳扎稳打”，逐路径走到底，把走过的路全部标记，最坏的情况也不过是把整个迷宫探索一遍，总能走出去。后者其实就是深度优先搜索算法的基本思想。

我们以更加“程序化”的语言描述一下使用深度优先搜索算法找到走出迷宫路径的方法：首先，选择迷宫入口作为“根节点”，发现两条岔路，将其中一条岔路压入栈中，选择另外一条岔路往下走，并且把走过的路径全部放在栈中，如果走到死胡同，就回溯，找到栈中还没有探索过的岔路，顺着该岔路继续执行上述步骤。

关于栈（stack）这种数据结构，可以参考我之前的文章：[C++标准容器类栈的基本使用][2]。

上述使用深度优先搜索算法走出迷宫的过程可以参考下面这个动图。

![使用深度优先搜索算法走出迷宫][3]

深度优先搜索

不难看出，深度优先搜索的主要策略是尽可能深入到图形深处，但是和广度优先搜索算法一样，应避免重复搜索同一个节点，并且从前面提到的“迷宫问题”中可以发现，深度优先搜索算法适合使用栈这种数据结构来跟踪和保存节点。遵循这几个基本策略，不难得到实现深度优先搜索算法的基本步骤：

• 访问节点 s。
• 标记节点 s 已经被访问过。
• 递归的访问 s 的未被标记过的邻节点（子节点）。

可参考下示动图理解这一过程。注意，动图没有展示“标记”操作。

![深度优先搜索算法的实例动画][4]

稍稍再解释下该动图：

• 首先，选择根节点作为起始访问点。
• 发现访问点有三个子节点，将这三个子节点全部压入栈中。
• 从栈中弹出一个节点（也即图示中的 2），把它作为访问点。
• 发现访问点有一个子节点，将这个子节点压入栈中。
• 从栈中弹出一个节点（也即图示中的 3），把它作为访问点。
• 发现访问点有一个子节点，将这个子节点压入栈中。
• 从栈中弹出一个节点（也即图示中的 4），把它作为访问点。
• 发现访问点没有子节点了，这次没有节点被压入栈中。
• 从栈中弹出一个节点（也即图示中的 5，这一过程便是所谓的“回溯”），把它作为访问点。
• 重复上述过程。

上述解释没有显式的“标记”操作是因为采用了栈数据结构——访问过的点直接就被丢弃了，这一过程可视为“标记”，因为它避免了访问过的点被重复访问。实际应用中，应该根据具体需求，设计具体的“标记”操作。

在上述操作中，遇到多个节点时，我们将所有节点都压入栈，读者可以思考，按照动图中的访问次序，多个节点的压栈顺序是怎样的呢？

实现深度优先搜索算法的伪代码

请看：

初始化空栈 s
将根节点压入 s
while s 不为空：
    从 s 弹出节点，作为访问节点
    处理访问节点
    for 所有的子节点 w of 访问节点：
        将 w 压入 s

编写C++代码解决“迷宫问题”

为了方便，我们以更加程序化的语言重新定义下“迷宫问题”：

定义一个二维数组 maze，使用 maze 表示一个迷宫：'o' 表示路，'+' 表示墙，左上角是入口，右下角是出口，只能横着或竖着走，不能斜着走，编写C语言程序从迷宫入口走到出口。

char maze[5][5] = {
    'o', '+', 'o', 'o', 'o',
    'o', '+', 'o', '+', 'o',
    'o', 'o', 'o', 'o', 'o',
    'o', '+', '+', '+', 'o',
    'o', 'o', 'o', '+', 'o',
};