动态规划算法有什么用?使用C语言编程解决一个实际问题,通俗易懂的学习动态规划法
发表于: 2020-02-24 16:49:00 | 已被阅读: 964 | 分类于: 算法
[上一节][1]讨论了程序开发中常用的分治算法,我们总结出使用该算法的其中一条“适用条件”为:原始问题可以拆分为**彼此独立**的子问题。这个条件其实不是使用“分治算法”的必要条件,只不过若子问题有重叠,分治算法会做许多不必要的重复工作,它会反复的求解那些公共的重叠子子问题。因此,如果子问题有重叠,一般不再推荐使用分治算法,可以考虑动态规划。
动态规划的基本思想
动态规划与分治算法相似,都是通过组合子问题的解来获得原始问题的解。只不过与分治算法不同,动态规划特别适合应用于子问题重叠的情况,它对每个子子问题只求解一次,并将解保存,之后求解其他依赖该子子问题的问题时,只需要从保存的结果中找出对应的解即可,这样就避免了反复求解公共的重叠子问题。
由此可以看出,动态规划算法本质上是牺牲部分空间换取时间效率。
钢条切割问题
上面的内容有些枯燥,来看一个实际问题:某公司的主营业务是购买长钢条,将其切割成短钢条出售。已知切割工序本身的成本可以忽略不计,不同长度单位的钢条价格如下表:
长度 i|1|2|3|4|5|6|7|8|9|10|... ---|--- 价格 p
假设有一段长度为 n 的钢条,问怎样切割才能获得最大的收益?
从钢条价格表可以看出,切割方案都是整数单位切割,对于长度为 n 的钢条,每个单位位置处都有 2 种可能(切,不切),因此总共有 2

容易看出,把长为 4 的钢条切割成 2 个长为 2 的钢条时,能够获得最大的收益为 5+5=10。
暴力穷举法
暴力穷举法的确能够解决问题,但是却不一定能够获得满意的效率。前面提到,对于长度为 n 的钢条有 2
令最优解为收益最大,为了便于讨论,我们使用加法符号“+”表示切割方案,例如 4 = 2+1+1 表示将长度为 4 的钢条切割为三段长分别为 2、1、1的短钢条。因此对于长度为 n 的钢条,假设一个最优解是将钢条切割为 k 段,那么对应的切割方案为:
n = i
1+ i2+...+ ik
最优切割方案确定后,最大的收益也就确定了——直接查表即可,设长度为 n 的钢条对应的最大收益为 mp
mp
n= pi1+ pi2+...+ pik
一个容易想到的解决方法是:从钢条左边切割下长度为 i 的一段,右边余下的钢条长度为 n-i,左边的钢条不再分割,只对右边的钢条递归继续分割。然后我们让 i 从 1 遍历到 n,也就遍历了所有的分割方案,遍历过程中,保存最大收益,即可得到解,使用数学公式描述这一过程,也即:
mp
n= max(pi+ mpn-i),其中 1≤i≤n
现在我们使用C语言编写程序来实现上述算法,使用递归是方便的:
int p[N] = {0,1,5,8,9,10,17,17,20,24,30...
int max_price(int n)
{
if (0==n)
return 0;
int mp = -1, i;
for (i=1; i<=n; i++) {
mp = max(mp, p[i]+max_price(n-i));
}
return mp;
}
如果读者读过我之前的文章,就应该明白对于C语言中的递归函数,我们更应该从实际需求角度分析它。max_price() 函数接收整数 n,返回长度为 n 的钢条的最大收益。若 n=0,不可能有任何收益,所以直接返回 0。接着,我们定义了变量 mp 用于存放最大收益,因为接下来要取它和分割方案对应的收益(大于0),所以给 mp 赋了负值作为初值。接下来的 for() 循环其实就是在描述公式 mp
读者可自行编写 main() 函数测试 max_price(),会发现 max_price(n) 函数的确能够正确计算长度为 n 的钢条最大收益值,例如 max_price(4)=10,max_price(10)=30。
不过解决问题倒不难,难点在于要“有效率”的解决问题,读者可自行测试,随着输入给 max_price() 的参数值逐渐增大,函数执行消耗时间急剧增加。在我的电脑上,max_price(16) 消耗 112ms 的时间,max_price(17) 消耗 332ms 的时间,每将 n 提升 1,函数执行时间就翻一倍多,当 n=30 时,我甚至没有耐心等下去了(我等了10多分钟,函数还没有执行完成)。
可见,暴力穷举法容易想到,也容易实现,但是却往往不能带来足够令人满意的效率。仔细考虑一下,应该不难发现,暴力穷举法的效率之所以如此低下,主要是因为中间产生了很多不必要的重复计算。请看下图:
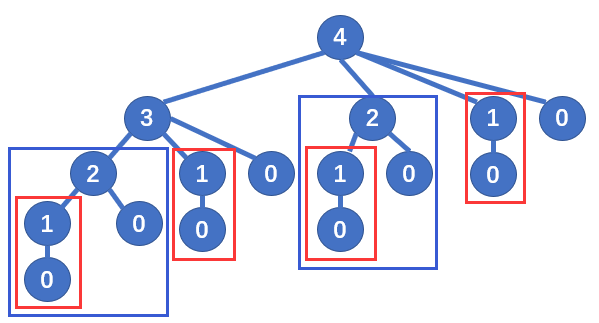
以 n=4 规模的求解为例,n=2 规模(蓝框)的求解会被更大规模(n=3、4)的求解重复计算,同理,n=1 规模(红框)的求解则会重复更多次。当 n 更大时,这些重复计算会越来越多,不难证明,随着 n 的增加,max_price() 函数的工作量会指数爆炸式的增长。
动态规划法
前文分析到,暴力穷举法之所以效率低下,根本原因在于执行了许多不必要的重复计算,如果能够避免这些重复计算,那么算法的效率必定会得到大大的提升。一个容易想到的方法是每计算一个子问题,就把该子问题的解存储起来,下次需要求解该子问题时,直接查询即可,从而避免重复计算。这其实就是动态规划法的基本思想。
时间效率对比
为了有更直观的感受,下面将对比本文实现的三种算法的时间效率,读者应该将注意力放在算法消耗时间的相对值上,绝对值在不同机器上是没有意义的。
n|暴力穷举法|动态规划法1|动态规划法2 ---|--- 10|1ms|1ms|1ms 15|39ms|1ms|1ms 16|110ms|1ms|1ms 17|325ms|1ms|1ms 30|>2min|1ms|1ms 5000|-|72ms|51ms 1万|-|301ms|283ms
三种算法的时间效率差异已经一目了然了我使用的计量单位最小为 1ms,在 n 等于 30 时,暴力穷举法的时间超过 2 分钟是因为我等待了两分钟还没有结果,我没有耐心,提前结束它了,实际的时间应该远大于 2 分钟。
另外,动态规划法 1 由于使用了递归处理,所以当 n 很大时,将消耗完堆栈空间,导致程序出现段错误。
小结
无论是上一节介绍的分治算法,还是本节讨论的动态规划算法,都是再程序开发中设计高效算法的基础。其实稍稍思考一下,应该不难发现,我们在获得时间高效率的时,通常都是要付出消耗更多空间的代价的,“天下没有免费的午餐”,这样的思想其实也可以应用于程序开发中。在之后的学习中,我们将对此观点的认识更加清晰。
max_price() 函数仅给出了最大的收益,如何添加代码输出对应的分割方案,留个读者自己考虑了。