文章目录

鱼眼图像矫正原理，成像模型，边缘畸变严重的解决方案，以及Python代码实现

		发表于: 2024-11-24 16:07:00 | 已被阅读: 195 | 分类于: 图像处理基础

0 鱼眼图像

鱼眼图像是一种特殊的宽视角成像方式，广泛应用于监控、全景摄影、机器人视觉等领域。鱼眼镜头的视角通常在 180° 或更大，远超普通镜头，因此可以捕捉到更大范围的场景。要做到这一点，鱼眼图像通常以非线性方式将场景投影到图像平面上。直线物体在图像中通常被呈现为弯曲的曲线。

图1. 鱼眼图像

图1是一张普通的鱼眼图像，可以看出鱼眼图像通常具有显著的圆形边界，中心区域接近真实场景，边缘部分则畸变严重。（刘冲的博客blog.popkx.com原创，偷文可耻）

1 鱼眼镜头的投影模型

在鱼眼相机中，为了将光线成像于一个平面上，一般会使用包含凸透镜、凹透镜和滤光镜在内的多种光学透镜，以减小入射光线的入射角。图1展示了鱼眼透镜（美国专利4,412,726）的布局以及光线复杂的入射或折射关系。

图2. 鱼眼镜头的投影模型

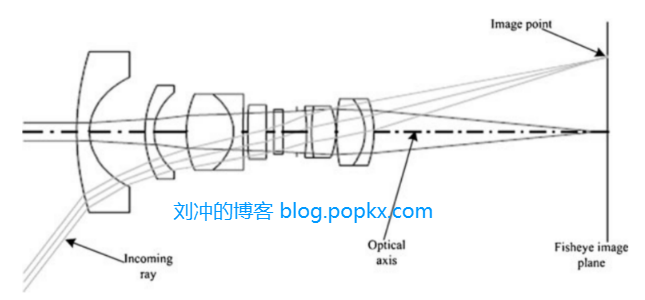
可以看出，光线的入射角经过透镜组后变小了，因此鱼眼镜头可以拍摄视场角更大的图像。鱼眼镜头的投影模型总体可以按照图3（b）简化：

图3. (a) 鱼眼镜头的几个数学投影模型（r=1）；(b)简化后的鱼眼镜头投影模型，点P按照针孔投影点为 p'，按照鱼眼镜头投影点为 p

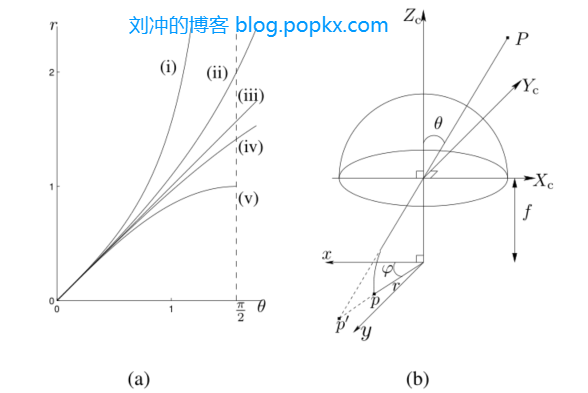
设 $ \theta $ 是主轴与入射光线之间的夹角，$ r $ 是像点与主点之间的距离，$ f $是焦距。鱼眼镜头的投影模型通常执行以下数学建模：

i. 透视投影 $ r = f*tan(\theta) $，针孔成像模型
ii. 正交投影 $ r = f*sin(\theta) $，将光线沿着球面投影到平面，适合小视角
iii. 等距投影 $ r = f * \theta $，投影的半径与光线的入射角度成比例
iv. 立体投影 $ r = 2f*tan(\frac{\theta}{2}) $，常用于全景摄影和球面投影
v. 等面积投影 $ r = 2f*sin(\frac{\theta}{2}) $，保持像素点的面积与球面面积成比例

在应用中，精心设计的镜头并不完全遵循设计的投影模型，实际成像过程可以看作理想投影的近似，既然是近似，我们可以找到一种更通用的近似： $$ r(\theta) = k_1\theta + k_2\theta ^ 3 + k_3 \theta ^5 + k_4 \theta ^7 + ... $$

2 鱼眼图像矫正

要对鱼眼图像矫正，需要先了解镜头的基本成像过程。我们回顾图3(b)，在针孔成像过程中，点 $ P $ 与光心，以及其成像点$ p' $三点共线，因此针孔相机拍摄的图像是没有畸变的。再看鱼眼成像过程，点$ P $发出的光线在经过鱼眼镜头后弯折，根据第 1 节中的内容，弯折程度与 $ \theta $ 相关，因此鱼眼图像是存在畸变的，并且越靠近图像边缘，畸变程度越高。（刘冲的博客blog.popkx.com原创，偷文可耻）

可以想象，如果我们将成像点 $ p $ 弯折到点 $ P $ 与光心的延长线上，弯折过程成像点 $ p $ 将划过一段曲线，所以针孔成像和鱼眼成像过程又可以按照图4简化：

图4. 针孔成像与鱼眼成像简化过程，鱼眼成像过程中原本弯曲的光线“拉直”后，等效为成像面弯曲为曲面

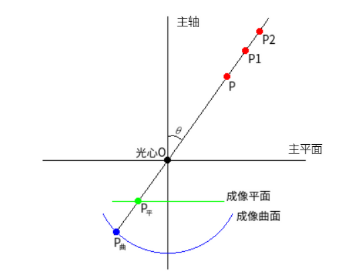
设$ P_平 $到主平面的距离为 $ f_平 $（成像平面的焦距），那么 $ P_平 $ 沿着成像平面到主轴的距离可以间的计算出来：

$$ L_平 = f_平 * tan(\theta) \tag{1} $$

$ P_曲 $沿着成像曲面到主轴的距离与鱼眼镜头的设计有关，如果鱼眼镜头是按照等距投影设计的，则：

$$ L_曲 = f_曲 * \theta \tag{2} $$

其中 $ f_曲 $表示成像曲面的焦距，也即$ P_曲 $到光心$ O $的距离。

通常，无论是针孔成像过程，还是鱼眼成像过程，都可以认为是各向同性的，所谓各向同性，可以粗略理解为：“像素坐标沿横轴的变化量等于纵轴的变化量”。因此有

$$ \frac{x_P}{y_P} = \frac{x_{P_平}}{y_{P_平}} = \frac{x_{P_曲}}{y_{P_曲}} \tag{3} $$

注意，图4并不是 xOy 平面，xOy 平面与成像平面平行。

俯视主平面，如图5所示：

图5. 俯视图4的主平面，各个点位于同一方向向量上

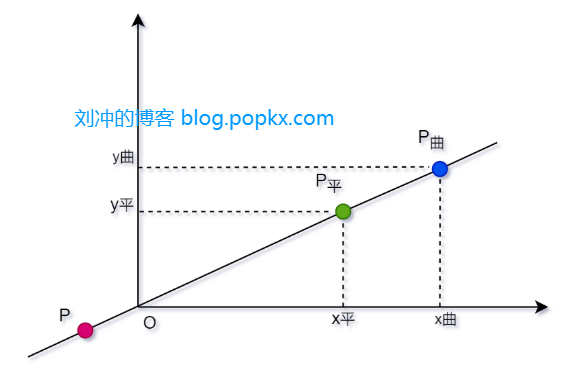
公式(3) 的意义是显然的——点 $ P $，$ P_平 $，$ P_曲 $ 位于同一个方向向量上，这意味着点 $ P $ 在成像平面上的像点与其在成像曲面上的像点仅有距离的区别，并且很容易得到从成像曲面中的坐标到成像平面中的坐标的转换关系，根据相似三角形，可得：

$$ x_曲 = x_平 * \frac{L_曲}{L_平} \\ y_曲 = y_平 * \frac{L_曲}{L_平} \tag{4} \\ L_平 = \sqrt{x_平^2 + y_平^2} $$

结合公式 (1)(2)(4)，可得以下关系：

$$ x_曲 = x_平 * \frac{f_曲 * arctan(\frac{L_平}{f_平})}{L_平} \\ y_曲 = y_平 * \frac{f_曲 * arctan(\frac{L_平}{f_平})}{L_平} \tag{5} $$

公式(5)构建了成像平面与成像曲面之间像素坐标的关系，这是本文执行鱼眼图像矫正的理论基础。

3 工程实现

第2节推导出的公式(5)已经是非常具体的方案，在具体实现中，可以先构建矫正后的图像，图像的像素按照坐标依次根据公式(5)换算到源鱼眼图像像素坐标，查询填入，简单的 Python 实现代码如下：

import numpy as np

def decode_fisheye(src, size, plane_focal_len, func_fisheye_model, func_get_pixel):
    h, w = src.shape[:2]
    dst_w, dst_h = size
    src_center_x, src_center_y = w / 2, h / 2
    dst_center_x, dst_center_y = dst_w / 2, dst_h / 2

    dst = np.zeros((dst_h, dst_w, src.shape[2]), dtype=src.dtype)

    for dst_y in range(dst_h):
        dst_row = dst[dst_y]
        dst_dy = dst_y - dst_center_y
        for dst_x in range(dst_w):
            dst_dx = dst_x - dst_center_x
            dst_l = np.sqrt(dst_dx**2 + dst_dy**2)

            theta = np.arctan(dst_l / plane_focal_len)
            src_l = func_fisheye_model(theta)

            k = 0.0 if dst_l == 0 else src_l / dst_l

            src_dx, src_dy = k * dst_dx, k * dst_dy
            src_x = src_center_x + src_dx
            src_y = src_center_y + src_dy

            func_get_pixel(dst_row, dst_x, src, src_x, src_y)
    return dst

func_fisheye_model() 为鱼眼成像的数学模型，例如选择第1节中介绍的几种模型之一。func_get_pixel()是查询填入过程使用的，可以使用最近邻方法或者双线性方法。为了方便使用，可以进一步封装：

class FisheyeCorrection(object):
    def __init__(self, cfg_dict: dict):
        self.plane_focal_len = cfg_dict['plane_focal_len']
        self.fisheye_focal_len = cfg_dict['fisheye_focal_len']

    def correct(self, img, output_size=(800, 600)):
        corrected_image = decode_fisheye(
            img, output_size, self.plane_focal_len, self.__fisheye_model, bilinear_interpolation)
        return corrected_image

    def __fisheye_model(self, theta):
        # common models
        # r = 2 * f * tan(theta / 2)
        # r = f * theta
        # r = 2 * f * sin(theta / 2)
        # r = f * sin(theta)
        return self.fisheye_focal_len * 2 * np.sin(theta / 2.0)

其中 bilinear_interpolation() 为双线性插值方法：

def bilinear_interpolation(dst_row, dst_x, src, src_x, src_y):
    h, w, c = src.shape
    if np.isnan(src_x) or np.isnan(src_y) or src_x < 0 or src_x >= w - 1 or src_y < 0 or src_y >= h - 1:
        dst_row[dst_x] = 0
        return
    left = int(np.floor(src_x))
    top = int(np.floor(src_y))
    w_right = src_x - left
    w_bottom = src_y - top
    w_left = 1 - w_right
    w_top = 1 - w_bottom

    weights = np.array([[w_left * w_top, w_right * w_top],
                        [w_left * w_bottom, w_right * w_bottom]])
    values = np.zeros(c)
    for dy in range(2):
        y = top + dy
        for dx in range(2):
            x = left + dx
            weight = weights[dy, dx]
            values += weight * src[y, x]
    dst_row[dst_x] = values.astype(src.dtype)

编写测试代码：

import cv2

...


def test():
    fisheye_correction_dict = {
        'plane_focal_len': 120,
        'fisheye_focal_len': 500
    }
    undistorted_img_size = (600, 400)
	
    fe_corr = FisheyeCorrection(cfg_dict=fisheye_correction_dict)

    img = cv2.imread('./test_fisheye.jpg')
    if img is None:
        print('img is empty.')
        return
    und_img = fe_corr.correct(img, undistorted_img_size)
    cv2.imshow('corrected', und_img)
    cv2.waitKey(0)

if __name__ == '__main__':
    test()

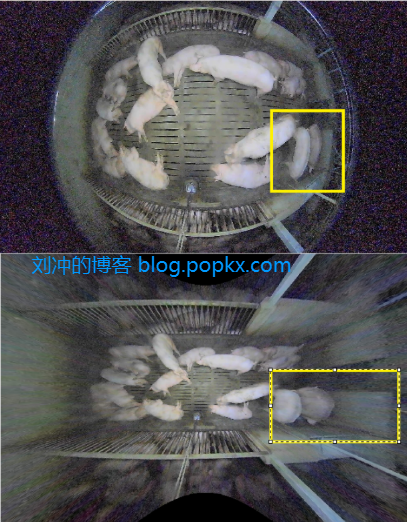
运行结果如图6所示，可见，鱼眼图像总体被拉平了，调整成像平面焦距和成像曲面焦距可以调整矫正程度。但是无论怎样调整，靠近图像边缘的内容畸变较大，例如黄框中的猪明显变形，这说明我们使用的鱼眼成像模型不够精确。（刘冲的博客blog.popkx.com原创，偷文可耻）