在参数空间叠加平均深度学习网络模型，进一步提升模型的泛化性能

本文受启发于 SWA，但是文章的主要内容基本都是个人理解。

梯度下降法

设深度学习网络的参数为 w，x 表示输入样本，损失函数为 L(x;w)，则“训练”该网络的过程，就是找到让 L(x;w) 最小的 w 的过程。因此，深度学习网络的核心本质是数学运算，而“训练”过程便是解数学方程的过程。

只不过，深度学习网络构建的数学方程式过于复杂，我们几乎不可能得到数学解析解，因此只能采用间接的方法求解，一个常用的求解方法便是梯度下降法:

w_{n+1} = w_n - \eta \nabla_w L(x;w_n) \tag 1

从公式 (1) 能够看出，梯度下降法是一个迭代更新参数的方法，更新的方向由损失函数的梯度方向决定，更新步长则由学习率 \eta 和梯度共同决定。（blog.popkx.com原创，未经许可抄袭可耻。）如果在迭代更新网络参数的过程中陷入了局部最小点，那么迭代更新就可能无法得到全局最小点，也即无法训练得到最优的深度学习网络模型。

如果训练过程跳过了所有局部最小点，得到了全局最小点，是否就得到完美性能的模型了呢？

通常，我们能够收集来训练深度学习网络的数据集 X 只是实际问题涉及数据 R 的一个很小的子集（例如我们一般不可能收集所有人的人脸图像用于训练人脸识别模型），所以：

\nabla_w L(X;w_n) - \nabla_w L(R;w_n) = \xi_n \tag 2

公式 (2) 给了我们启发：\xi_n 的存在使得训练得到的 w 不是确定值，而是一个概率分布。为了让最终得到的模型具备更好的泛化性能，只能让收集到的数据集 X 的数据分布尽可能的与 R 保持一致，这其实就是数据增强能够提高模型泛化能力的的主要原因之一。

不过，即使是数据增强也不能让 X 与 R 的数据分布完全一致，所以深度学习网络模型的训练即使达到最优，即找到了 L(x;w) 的全局最小值，也不能保证模型应用到实际问题时，具有模型在 X 上同样优秀的性能。

干扰深度学习模型泛化性能的两大因素

总结一下前文就是，在使用梯度下降法训练深度学习网络模型的过程中，会受到两大因素的干扰，阻碍我们得到泛化性能优秀的模型：

损失函数的局部最小因素；
训练数据集只是实际问题涉及数据的子集因素。

第 1 个因素可以通过各种手段尽量避免（比如 SGD 优化策略，设计各种带动量的优化器）；（blog.popkx.com原创，未经许可抄袭可耻。）第 2 个因素却是致命的：找到损失函数 L(x;w) 的全局最小点是设计训练方法的（可以说唯一）参考，如果这个参考不能保证得到泛化性能最优秀的深度学习网络模型，那么我们甚至连优化改进的方向都没有。

损失函数曲线

从公式 (2) 来看，若是将损失函数 L(x;w) 运用到 R 上，则在 X 的数据分布与 R 相似的区域，损失函数值较小。在数据分布差异较大的其他区域，因为 \xi_n 较大，每次实际的迭代优化偏差较大，难以稳定降低损失函数 L(x;w)，所以损失值较大。

粗略来看，若是将损失函数在各个样本上的损失值连接起来，可以得到一条损失曲线：

这里要注意横轴表示的是数据分布，按照我们的分析，损失曲线在 X 的分布区域会出现一个谷。

一般来说，用于测试训练完毕的深度学习模型的测试数据集 Y 与 X 的交集为空，但是二者的数据分布却总体上相似，略有差异（通常来自同一批收集），因此若将损失函数也同时运用到 Y，直观上来看就如下图所示：

通常，损失函数值越小，表明深度学习网络模型的预测越准确，所以就上图而言，可以断定在测试集 Y 上，模型对集中在谷底区域对应的样本预测最准确，而对橙色曲线最右端对应的样本预测最差。

这样的发现给了我们启发：若深度学习网络模型在训练阶段的损失函数曲线是一个非常“尖锐”的曲线，那么它的总体泛化性通常较差，反之，若是损失函数曲线比较“平坦”，那么它的总体泛化性能一般较好。

看来，要优化因素 2 带来的泛化性能干扰，也不是全无头绪。

稍稍再思考一下，尖锐的损失曲线一般什么时候产生呢？（blog.popkx.com原创，未经许可抄袭可耻。）我觉得使用梯度下降法迭代更新减小 L(x;w) 时，若是陷入了局部最小，则最终 L 只在“某一个小区域”较小，我们便相当于得到了“尖锐”的损失曲线。

实例分析

上一小节中的“损失曲线”图非常简单，只是便于直观理解的示意图。读者应该明白，现实问题涉及的数据分布一般非常复杂，数据分布-损失值曲线图通常不是变化缓和的光滑曲线，不过我们得到的启发却是通用的。

在实践中，我训练了一个检测人脸信息的深度学习网络模型。上图是我遇到的一个问题，请看人脸预测框右侧倒数第 2 个数字，它表示人脸颊被遮挡的概率。虽然左右两张图片的内容非常相似（直觉上认为它们的数据分布接近），但是我训练的深度学习网络模型对二者的预测结果却有较大差异。

通过上一小节的讨论，我们可以推测出现这种情况的原因：我训练的深度学习网络模型的损失函数曲线在谷底不够平坦，上面两张图的数据分布恰好处于损失曲线的拐点附近，右图位于谷底，而左图则在损失值较大的位置。可以参考下示意图：

获取更平坦的“谷底”

通过前面的分析，我们知道要优化因素 2 带来的泛化性能干扰，获取具有更加平坦“谷底”的损失函数曲线是一个可行方案。

但是从数学上来看，获取具有更加平坦“谷底”的损失曲线是一件非常不容易的事，我们甚至连衡量深度学习网络模型损失曲线是否“平坦”的标准都没有，方法就更不用提了。（blog.popkx.com原创，未经许可抄袭可耻。）不过，从简化后的示意图来看，倒是有一些启发性的思路。

鉴于深度学习网络通常构建的是比较复杂的数学运算，而我们训练一般使用随机梯度下降法，所以，即使是同一个网络结构，使用不同的随机初始化，不同的训练过程，最终得到的损失曲线也是可能有差异的（总体相似）。

如上示意图所示，网络 1 和网络 2 的网络结构相同，训练过程不同——也即参数不同，因此二者的损失曲线总体相似，但是有差异，若是我们叠加二者的损失曲线，则可以得到谷底更加平坦的曲线。更进一步的，随着参与叠加的网络数目的增加，最终得到的损失曲线谷底也会随之变得愈发平坦。这个启发性的思路与直觉相符：多个网络参与预测的结果趋于更加稳定。

三个臭皮匠，顶个诸葛亮。

时间效率

叠加多个深度学习网络模型的输出，以获得更加平坦的损失曲线，进而得到更优异的泛化性能是可行的。但是有一个问题：随着参与叠加网络数目的增加，整体网络模型的推理消耗（时间、内存等）也在成倍增加，这对于一些资源紧张，或者注重时间效率的任务来说难以接受。

有没有办法加速呢？自然是有的，只不过要损耗一些网络模型参数的动态范围。令 m 表示网络模型结构，w_i 表示第 i 个训练对应的网络参数，具备更平坦谷底的损失曲线的叠加平均网络模型为 \bar m。

温馨提示：
输入邮箱或者手机号码，付款后可永久阅读隐藏的内容，请勿未经本站许可，擅自分享付费内容。
如果您已购买本页内容，输入购买时的手机号码或者邮箱，点击支付，即可查看内容。
电子商品，一经购买，不支持退款，特殊原因，请联系客服。 付费可读

进一步训练网络

深度学习网络模型即将收敛时，减小优化器的学习率是一个普遍使用的技巧，这有助于模型稳定收敛。（blog.popkx.com原创，未经许可抄袭可耻。）但是，减小学习率的同时，优化器陷入局部最小点的可能性就增加了，按照前文的讨论，这将导致得到“尖锐”损失曲线的可能性增加，影响模型的泛化性能。

上图是我遇到的一个实践问题，我训练的人脸信息检测深度学习网络模型对这张图的检测效果始终不好——图中的人眼部明显被遮挡了，但是模型预测的遮挡概率值几乎为零。最关键的是，无论我如何继续训练，损失函数值如何降低，模型对该图的眼部遮挡预测始终无响应。

当然了，模型对于其他大多数样本的预测都是准确的。推测原因，应该是优化器陷入局部最优点了，因此我们得到了“尖锐”的损失曲线，上图位于损失曲线的高位。所以只有优化器跳出局部最优点，模型对该图预测才可能准确。但是，即使优化器跳出了当前的局部最优点，我们也不能保证它不陷入另一个局部最优点——对另外一些图预测不准确。

所以，只使用单个模型进一步提升泛化性能的难度很大，因此考虑使用前文讨论的“叠加平均法”，我们优先考虑使用 m(\bar w)（鉴于它不额外消耗内存和推理时间）。

按照前文的讨论，若期望“叠加平均法”能够得到更优异的泛化性能，需要参与叠加平均的网络模型有差异，而陷入局部最优的优化器带来“差异”的能力有限，所以要使用“叠加平均法”，首先需要跳出局部最优点。

跳出局部最优点的一个直接可行手段是加大学习率，但是这会导致模型振荡，难以稳定收敛到理想值。（blog.popkx.com原创，未经许可抄袭可耻。）所以，使用大学习率训练网络模型跳出局部最小点后，仍然需要继续使用较小的学习率让网络模型稳定收敛。根据公式 (7)，若期望 m(\bar w) 正常工作，需要对损失函数添加正则项：

L'(x;w_i) = L(x;w_i) + \lambda ||\bar w - w_i||^2 \tag 8

其中 \bar w 根据公式 (4) 计算获得。公式 (8) 中的正则项与 \bar w 与 w_i 的绝对差值成正相关，因此减小 \bar w 和 w_i 自身的值有助于 L'(x;w_i) 的优化，这个操作是简单的，只需要在训练网络模型 m 时增加 L2 正则优化即可。

总结一下，在深度学习网络模型收敛后，我们仍然可以进一步提升其泛化性能：

为损失函数添加 L2 正则项和 ||\bar w - w_i||^2 正则项；
使用较大学习率训练模型若干次；
使用较小学习率训练模型多干次；
得到网络参数 w_i。

得到若干个 w_i 后，根据公式 (4) 得到 \bar w，进而得到泛化性能更优秀的 m(\bar w)。

步骤2、3中的“较大”学习率需要多大，“较小”学习率需要多小，“若干次”是多少次呢？目前这个内容正在申请专利，后续再公开讨论吧。

优化效果

以我训练的深度学习网络模型为例，在模型收敛后，继续使用前面讨论的方法继续训练，其在测试集上的表现如下图所示：

上图中的横轴是参与计算 \bar w 的 w_i 个数，纵轴是模型在测试集上的预测综合准确率。

单个模型收敛时，综合准确率基本维持在 0.975 左右。使用本文讨论的方法继续训练模型，当参与计算 \bar w 的网络个数为 2 时，模型的泛化性能有一个突降。（blog.popkx.com原创，未经许可抄袭可耻。）猜测可能是因为首次使用大学习率优化器跳出了局部最优点的缘故，测试时模型尚未到达另外的最优点。不过，随着继续训练的进行，参与计算 \bar w 的 w_i 数目的增加，模型泛化性能稳步提升，最终取得更加优异的泛化性能。

我们使用最终得到的 m(\bar w) 测试之前两组误检的图片，得到如下结果：

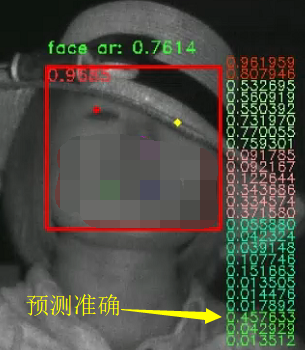
可见，m(\bar w) 确实进一步提升了模型的泛化性能。